KCET 2019 Maths Paper with Solutions

Introduction to KCET 2019 Maths Paper

The Karnataka Common Entrance Test (KCET) is an annual examination conducted for admission to various undergraduate courses in colleges across the state of Karnataka, India. Among the subjects tested, Mathematics holds significant importance due to its weightage and relevance in many courses. The KCET 2019 Maths paper was a crucial aspect of the exam, assessing students’ proficiency in mathematical concepts and problem-solving skills.

Detailed Analysis of KCET 2019 Maths Paper

The KCET 2019 Maths paper was a comprehensive test covering a wide range of topics from algebra to calculus. Students found the paper to be moderately difficult, with a balanced distribution of questions from different areas of mathematics. Notable questions included those involving applications of trigonometry, calculus, and geometry. The feedback from students indicated that while some questions were challenging, others were manageable with thorough preparation.

Algebra

One of the key areas in the KCET Maths paper was algebra. Questions ranged from basic algebraic equations to complex polynomial expressions. By applying fundamental algebraic principles, students could effectively solve these questions and arrive at the correct answers.

Trigonometry

Trigonometry questions in the KCET 2019 Maths paper required students to apply trigonometric ratios and identities to solve problems related to angles and triangles. Through a clear understanding of trigonometric concepts, students could navigate through these questions efficiently.

Calculus

Calculus questions tested students’ understanding of differentiation, integration, and their applications. By employing calculus techniques, students could tackle problems involving rates of change, areas under curves, and optimization, among others.

Geometry

Geometry questions encompassed topics such as circles, triangles, and polygons. By utilizing geometric properties and theorems, students could solve problems related to areas, volumes, and angles with precision.

Question 1: If

\begin{array}{l} \sqrt[3]{y} \sqrt{x} = \sqrt[6]{(x + y)^{5}} \end{array}

, then dy/dx equal to:
a. x/y
b. x+y
c. x-y
d. y/x
Answer:(d)

\begin{array}{l} \sqrt[3]{y} \sqrt{x} = \sqrt[6]{(x + y)^{5}} \end{array}

Apply log on both sides

log (y^1/3x^1/2) = log(x+y)^5/6

(1/3) log y+(1/2) log x = (5/6) log(x+y)

(1/3y)(dy/dx)+(1/2x) = (5/6(x+y))(1+dy/dx)

(1/3y)(dy/dx)- (5/6(x+y))dy/dx =(5/6(x+y)) -(1/2x)

(dy/dx)[(1/3y)-(5/6(x+y)] = 5x-3(x+y)/6x(x+y)

(dy/dx) = [(2x-3y)/6x(x+y)][6y(x+y)/(2x-3y)]

dy/dx = y/x

Question 2: Rolle’s theorem is not applicable in which one of the following cases?

a. f(x) = x²-4x+5 in [1, 3]

b. f(x) = x²-x in [0, 1]
c. f(x) = x in [-2, 2]
d. f(x) = [x] in [2.5, 2.7]

Answer:(c)

Check option:

Option (a):

(1) f(x) is continuous function in [1, 3]

(2) f(x) is differentiable in (1, 3)

Option (b):

(1) f(x) is continuous function in [0, 1]

(2) f(x) is differentiable in (0, 1)

Option (c):

(1) f(x) is continuous function in [–2, 2]

(2) f(x) is not differentiable at point x = 0 in (–2, 2)

Option (d):

(1) f(x) is continuous function in [2.5, 2.7]

(2) f(x) is differentiable in (2.5, 2.7)

Question 3: The interval in which the function f(x) = x³-6x²+9x+10 is increasing in

a. (-∞,1) ⋃ (3, ∞)

b. (-∞,-1) ⋃ (-3, ∞)
c. [1, 3]
d. (-∞,-1) ⋃ [3, ∞)

Answer:(b)

f(x) = x³-6x²+9x+10

Differentiate with respect to x

f’(x) = 3x²-12x+9

f’(x) ≥ 0

⇒ 3x²-12x+9 ≥0

⇒ x²-4x+3 ≥ 0

⇒ x²-3x -x+3 ≥ 0

⇒ (x-3) (x-1) ≥ 0

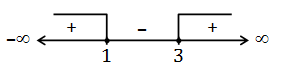
x ∈ (-∞, 1] ⋃[3, ∞ )

Question 4: The side of an equilateral triangle are increasing at the rate of 4cm/sec. The rate at which its area is increasing, when the side is 14 cm

a. 10√3 cm²/sec

b. 14√3 cm²/sec
c. 42 cm²/sec
d. 14 cm²/sec

Answer:(G)

Bonus

Question 5: The value of √24.99 is

a. 4.999

b. 4.899
c. 5.001
d. 4.897

Answer:(a)

f(x) = √x

⇒ dy/dx = 1/2√x

∆y = (dy/dx) ∆x …(i)

Here x = 25 and ∆x = 0.1

∆y = √x-√(x-∆x)

(dy/dx) ∆x = √25-√(25-0.1)

√24.99 = 5-(1/2×5)×0.1

= 5-0.01

= 4.99

Question 6: If 3x-5≤2 then

a. -1≤x≤7/3

b. 1≤x≤7/3
c. 1≤x≤9/3
d. -1≤x≤9/3

Answer:(b)

|3x-5| ≤ 2

⇒ -2 ≤3x–5 ≤ 2

⇒ 3 ≤ 3x ≤ 7

⇒ 1 ≤ x ≤7/3

Question 7: A random variable ‘X’ has the following probability distribution:

X	1	2	3	4	5	6	7
P(X)	k-1	3k	k	3k	3k²	k²	k²+k

a. 1/5
b. -2
c. 2/7
d. 1/10

Answer:(a)

∑P(K)=1

⇒ K-1+3K+K+3K+3K²+K²+K²+K = 1

⇒ 5K²+9K-2 = 0

⇒5K²+10K-K-2 = 0

⇒ (5K-1)(K+2) = 0

5K-1 = 0 or K+2 = 0

K = 1/5 or K = -2 (not possible)

Question 8: If A and B are two events of a sample space S such that P(A) =0.2, P(B) =0.6 and P(AB)=0.5 then P(A’|B)=

a. 3/10

b. 2/3
c. 1/2
d. 1/3

Answer:(c)

Given that

P(A) = 0.2

P(B) = 0.6

P(A|B) = 0.5

Now

P(A’|B) = 1-P(A|B)

= 1-0.5

= 0.5

= 1/2

Question 9: If ‘X’ has a binomial distribution with parameters n = 6, p and P(X = 2) = 12, P(X = 3) = 5 then P=

a. 5/12

b. 16/21
c. ½
d. 5/16

Answer:(G)

Bonus

*G indicates one grace mark

Question 10: A man speaks truth 2 out of 3 times. He picks one of the natural numbers in the set S = {1, 2, 3, 4, 5, 6, 7} and reports that it is even. The probability that it is actually even is

a. 2/5
b. 1/5
c. 1/10
d. 3/5

Answer:(d)

S = {1,2,3,4,5,6,7}

Total probability = 7

P(S₁) = Probability of even number = 3/7

P(S₂) = Probability of odd number = 4/7

P(ES₁) = 2/3

P(ES₂) = 1-2/3 = 1/3

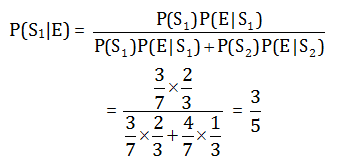
Question 11: If U is the universal set with 100 elements; A and B are two sets such that n(A) = 50, n(B) = 60, n(A⋂B) = 20 then n(A’⋂B’) = ?

a. 40

b. 20
c. 90
d. 10

Answer:(d)

Given that

n(A) = 50

n(B) = 60

n(A⋂B) = 20

Now

n(A’⋂ B’) = P(A⋂B)’

= 100-P(A⋂B)

= 100-[P(A)+P(B)- P(A⋂B)]

= 100-[50+60-20]

= 100-90

= 10

Question 12: The domain of the function f:R→R defined by f(x) = √(x²-x+12)

a. (-∞,3] ⋃[4, ∞)

b. (-∞,3] ⋃(4, ∞)
c. (-∞,3] ⋂ [4, ∞)
d. (3,4)

Answer:(a)

f(x) = √(x²-7x+12)

Now

x²-7x+12≥0

x²-4x-3x+12≥0

(x-4)(x-3) ≥0

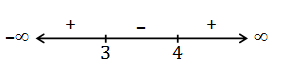
x∈(-∞,3] ⋃[4, ∞)

Question 13: If cos x = sin x then, the general solution is

a. x = nπ ± π/4, n∈Z

b. x = 2nπ ± π/4, n∈Z
c. x = nπ+(-1)ⁿ π/4, n∈Z
d. x = (2n+1)π ± π/4, n∈Z
Answer:(b)

cos x = |sinx|

Case-1:

cos x = sin x for x∈ [0, π ]

tan x = 1 for x = π/4

Case-2:

s x = -sin x for x ∈ [π, 2π]

tan x = -1 for x∈ 7π/4

Combining both the cases, we get the general is solution 2nπ±π/4

Question 14: √3 cosec 20⁰– sec 20⁰ =

a. 2

b. 3
c. 4
d. 1

Answer:(c)

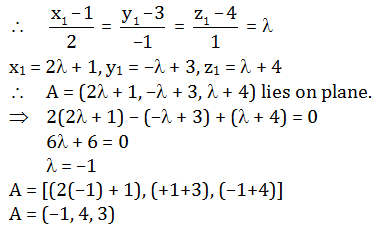
Question 15: If P(n): 2ⁿ<n! then the smallest positive integer for which P(n) is true, is

a. 2

b. 3
c. 4
d. 5

Answer:(c)

P(n): 2ⁿ< n!

Since

P(1): 2 < 1 is false.

P(2): 2²< 2! is false.

P(3): 2³< 3! is false.

P(4): 2⁴< 4! is true.

P(5): 2⁵< 5! is true.

So, the smallest positive integer is 4.

Question 16: Foot of the perpendicular drawn from the point (1,3,4) to the plane 2x-y+z+3=0 is

a. (-1,4,3)
b. (0,-4,-7)
c. (1,2,-3)
d. (-3,5,2)

Answer:(a)

The Dr’s of PA are

x₁-1, y₁-3, z₁-4

The Dr’s n are 2, -1, 1

The Dr’s of PA and n are parallel

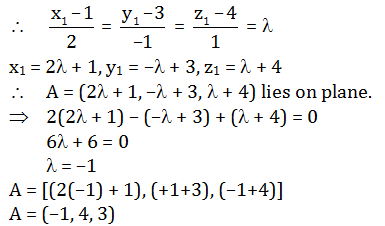
Question 17: Acute angle between the line (x-5)/2 = (y+1)/-1 = (z+4)/1 and the plane 3x-4y-z+5 = 0 is:

a. cos^-1(9/√364)
b. sin^-1(9/√364)
c. cos^-1(5/2√13)
d. sin^-1(5/2√13)

Answer:(c)

L: (x-5)/2 = (y+1)/-1 = (z+4)/1

Dr’s of line: 2, -1, 1

P: 3x-4y-z + 5 = 0

Dr’s of normal to plane: -3, 4, 1

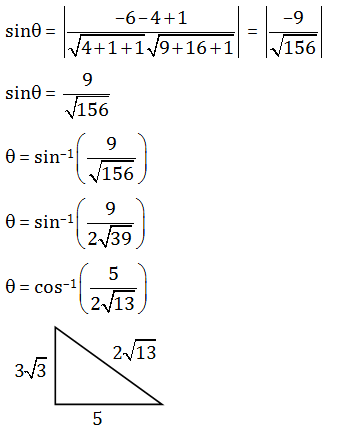
Question 18: The distance of the point (1,2,1) form the line (x-1)/2 = (y-2)/1 = (z-3)/2 is

a. 2√3/5

b. 2√5/3
c. √5/3
d. 20/3

Answer:(b)

Let L: (x-1)/2 = (y-2)/1 = (z-3)/2 = λ

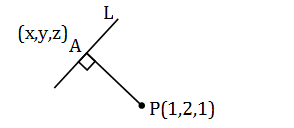
PA→

= Position vector of A – position of vector of P

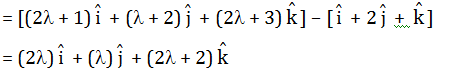
Vector PA perpendicular to L.

PA→.L=0

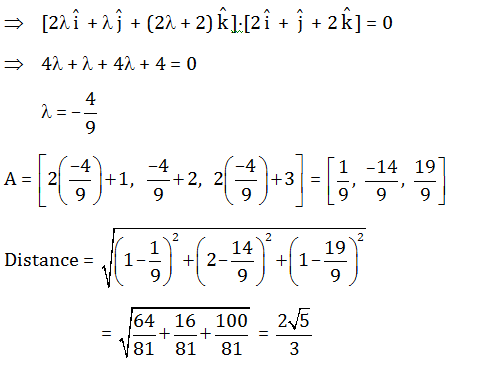
Question 19: XY-plane divides the line joining the points A(2,3,-5) and B(-1,-2,-3) in the ratio

a. 2:1 internally

b. 3:2 externally
c. 5:3 internally
d. 5:3 externally
Answer:(d)

A(2,3,-5), B(-1,-2,-3)

The ratio that xy plane divide line joining the points (x₁,y₁,z₁) and (x₂,y₂,z₂) = -z₁:z₂

If result is positive, it divides internally otherwise externally.

The ratio that xy plane divides the points (2,3,-5) and (-1,-2,-3)

= -(-5) :(-3)

= -5 : 3

So, 5 : 3 externally in the ratio.

Question 20: The shaded region in the figure is the solution set of the inequations

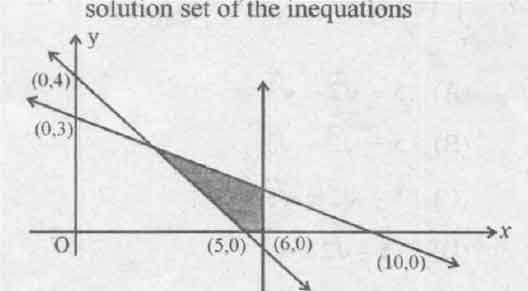
a. 4x+5y≥20, 3x+10y≤30, x≤6, x, y≥0.

b. 4x+5y≥20, 3x+10y≤30, x≥6, x, y≥0.
c. 4x+5y≤20, 3x+10y≤30, x≤6, x, y≥0.
d. 4x+5y≤20, 3x+10y≤30, x≥6, x, y≥0.

Answer:(a)

(1) Since the region lies above the x-axis

So y ≥0

(2) Shaded region is on right side of the y-axis

So x ≥0

(3) Equation of line passing through (5,0) and (0, 4) is

(y-0) = (4/-5) (x-5)

-5y = 4x- 20

4x+5y = 20

(4) Equation of line passing through (10,0) and (0, 3) is

(y-0) = (-3/10) (x-10)

-10y = 3x-30

3x+10y = 30

(5) Shaded region is on left of x = 6.

So x ≤6

Consider the figure and observe the shaded region the inequalities can be written as

x ≥ 0,

y ≥ 0,

x ≤ 6

4x+5y ≥20,

3x+10y ≤ 30

Question 21: The order of the differential equation is

y=C1eC2+x+C3eC4+x

a. 1
b. 2
c. 3
d. 4
Answer:(a)

y=C1eC2+x+C3eC4+x

Differentiate with respect to x

dy/dx =

C1eC2+x+C3eC4+x

dy/dx = y

(dy/dx)-y = 0

Hence the order is 1.

Question 22: If

\begin{array}{l} | \vec{a} | = 16 \end{array}

\begin{array}{l} | \vec{b} | = 4 \end{array}

, then

\begin{array}{l} \sqrt{{| \vec{a \times \vec{b}} |}^{2} + {| \vec{a} . \vec{b} |}^{2}} \end{array}

a. 4
b. 8
c. 16
d. 64
Answer:(d)

\begin{array}{l} | \vec{a} | = 16 \end{array}

\begin{array}{l} | \vec{b} | = 4 \end{array}

Now,

\begin{array}{l} \sqrt{{| \vec{a \times \vec{b}} |}^{2} + {| \vec{a} . \vec{b} |}^{2}} = \sqrt{{| \vec{a} |}^{2} {| \vec{b} |}^{2} \sin^{2} θ + {| \vec{a} |}^{2} {| \vec{b} |}^{2} \cos^{2} θ} \end{array}

\begin{array}{l} | \vec{a} | | \vec{b} | \sqrt{\sin^{2} θ + \cos^{2} θ} \end{array}

= 16×4×1

= 64

Question 23: If the angle between

a→

and

b→

2π3

and the projection of

a→

in the direction of

b→

is -2, then

|a→|

a. 4

b. 3
c. 2
d. 1
Answer:(a)

Given angle between

a→

and

b→

2π3

And

a→.b→|b→|=−2

⇒

|a→||b→|cos⁡θ|b→|=−2

⇒

|a→|cos⁡2π3=−2

⇒

|a→|×−12=−2

⇒

|a→|=4

Question 24: A unit vector perpendicular to the plane containing the vectors

\begin{array}{l} \hat{i} + 2 \hat{j} + \hat{k} \end{array}

and

\begin{array}{l} - 2 \hat{i} + \hat{j} + 3 \hat{k} \end{array}

is:

\begin{array}{l} \frac{\hat{i} + \hat{j} + \hat{k}}{\sqrt{3}} \end{array}

\begin{array}{l} \frac{\hat{i} + \hat{j} - \hat{k}}{\sqrt{3}} \end{array}

\begin{array}{l} \frac{- \hat{i} + \hat{j} - \hat{k}}{\sqrt{3}} \end{array}

\begin{array}{l} \frac{- \hat{i} - \hat{j} - \hat{k}}{\sqrt{3}} \end{array}

Answer:(c)

The vector which is perpendicular to two vectors is given by the cross product of the two vectors.

\begin{array}{l} \vec{P} \times \vec{Q} = (- 2 \hat{i} + \hat{j} + 3 \hat{k}) \times (\hat{i} + 2 \hat{j} + \hat{k}) \end{array}

\begin{array}{l} - 5 \hat{i} + 5 \hat{j} - 5 \hat{k} \end{array}

\begin{array}{l} | \vec{P} \times \vec{Q} | = \sqrt{5^{2} + 5^{2} + 5^{2}} = 5 \sqrt{3} \end{array}

Unit vector perpendicular to P and Q is given by

\begin{array}{l} C = \frac{\vec{P} \times \vec{Q}}{| \vec{P} \times \vec{Q} |} \end{array}

\begin{array}{l} \frac{- 5 \hat{i} + 5 \hat{j} - 5 \hat{k}}{5 \sqrt{3}} \end{array}

\begin{array}{l} \frac{- \hat{i} + \hat{j} - \hat{k}}{\sqrt{3}} \end{array}

Question 25:

\begin{array}{l} [\vec{a} + 2 \vec{b} - \vec{c}, \vec{a} - \vec{b}, \vec{a} - \vec{b} - \vec{c}] \end{array}

a. 0
b.

\begin{array}{l} [\vec{a}, \vec{b}, \vec{c}] \end{array}

\begin{array}{l} 2 [\vec{a}, \vec{b}, \vec{c}] \end{array}

\begin{array}{l} 3 [\vec{a}, \vec{b}, \vec{c}] \end{array}

Answer:(d)

\begin{array}{l} (\vec{a} + 2 \vec{b} - \vec{c}) \cdot {\vec{a} - \vec{b} \times \vec{a} - \vec{b} - \vec{c}} \end{array}

\begin{array}{l} (\vec{a} + 2 \vec{b} - \vec{c}) \cdot {- \vec{a} \times \vec{b} - \vec{a} \times \vec{c} - \vec{b} \times \vec{a} + \vec{b} \times \vec{c}} \end{array}

\begin{array}{l} [\vec{a} \vec{b} \vec{c}] - 2 [\vec{b} \vec{a} \vec{c}] \end{array}

\begin{array}{l} [\vec{a} \vec{b} \vec{c}] + 2 [\vec{a} \vec{b} \vec{c}] \end{array}

\begin{array}{l} 3 [\vec{a} \vec{b} \vec{c}] \end{array}

Question 26:

∫−33cot−1⁡xdx=

a. 3π
b. 0
c. 6π
d. 3

Answer:(a)

Let I =

∫−33cot−1⁡xdx

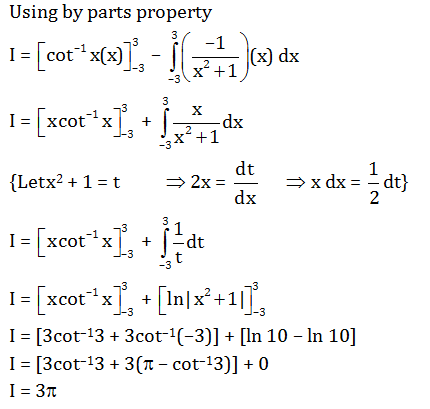
Question 26:

∫−33cot−1⁡xdx=

a. 3π
b. 0
c. 6π
d. 3

Answer:(a)

Let I =

∫−33cot−1⁡xdx

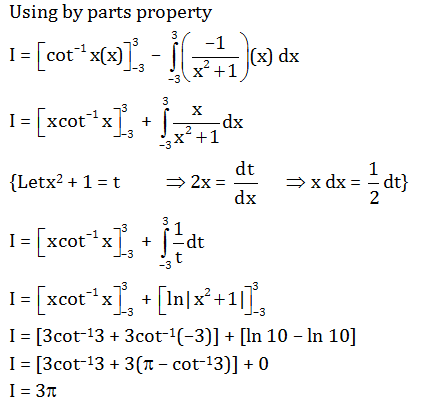
Question 27:

∫1x+xxdx=

a. 2 log (√x+1)+C
b. (½) tan^-1√x+C
c. tan^-1√x+C
d. 2 tan^-1√x+C

Answer:(d)

Let I =

∫1x+xxdx

∫1x(x+1)dx

Let √x = t

x = t²

dx = 2t dt

So I =

∫1t(1+t2)2tdt

I =

2∫1(1+t2)dt

= 2 tan^-1t +C

= 2 tan^-1√x+C

Question 28:

∫2x−1(x−1)(x+2)(x−3)dx=Alog|x−1|+Blog|x+2|+Clog|x−3|+K

, then A, B, C are respectively:

a. -1/6, 1/3, -1/2
b. 1/6, 1/3, -1/5
c. 1/6, -1/3, 1/3
d. -1/6, -1/3, 1/2

Answer:(d)

Let I =

∫2x−1(x−1)(x+2)(x−3)dx

Now,

(2x-1)/(x-1)(x+2)(x-3) = (A/(x-1) )+(B/(x+2))+(C/(x-3))

2x-1 = A(x+2)(x-3)+B(x-1)(x-3)+C(x -1)(x+2)

Putting x = 3, we get

6 -1 = C(3-1)(3+2)

C = ½

Putting x = 1, we get

2-1 = A(1+2)(1-3)

A = -1/6

Putting x = -2, we get

-4-1 = B(-2-1)(-2-3)

B = -1/3

A.B,C are -1/6, -1/3, 1/2.

Question 29:

∫02[x2]dx=

a. 5-√2-√3
b. 5+√2-√3
c. 5-√2+√3
d. -5-√2-√3

Answer:(a)

Let I =

∫02[x2]dx

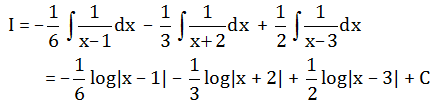
I = (√2-1)+2(√3-√2)+3(2-√3)

= √2-1+2√3-2√2+6-3√3

= 5-√2-√3

Question 30:

∫011+x1−xdx=

a. (π/2)-1 b. (π/2)+1 c. π/2 d. 1/2 Answer:(b) Let I =

∫011+x1−xdx

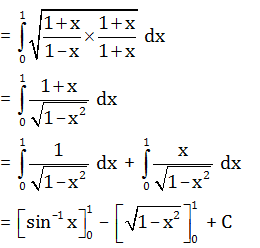= (π/2)-0-(0-1) = (π/2)+1

Question 31: If α and β are the roots of the equation x²+x+1 = 0 then α²+β² is:>

a. 1

b. (-1+i√3)/2
c. (-1-i√3)/2
d. -1

Answer:(d)

Given equation is x²+x+1 = 0

α+β = -1

αβ = 1

Now, α²+β² = (α+β)²-2αβ

= (-1)²-2(1)

= 1-2

= -1

Question 32: The number of 4-digit numbers without repetition that can be formed using the digits 1,2,3,4,5,6,7 in which each number has two odd digits and two even digits is

a. 432

b. 436
c. 450
d. 454

Answer:(a)

Given digits are 1, 2, 3, 4, 5, 6, 7

Two even digits can be selected in ³C₂

Two odd digits can be selected in ⁴C₂ ways

These selected 4 digits can be arranged in 4! ways

The total number of ways = ⁴C₂×³C₂×4!

= 6×3×24

= 432

Question 33: The number of terms in the expansion of (x²+y²)²⁵-(x²-y²)²⁵ after simplification is

a. 0

b. 13
c. 26
d. 50

Answer:(b)

(x²+y²)²⁵-(x²-y²)²⁵

(a+b)ⁿ-(a-b)ⁿ if n is odd

On simplification we get (n+1)/2 terms

i.e. (25+1)/2 = 26/2

= 13

Question 33: The number of terms in the expansion of (x²+y²)²⁵-(x²-y²)²⁵ after simplification is

a. 0

b. 13
c. 26
d. 50

Answer:(b)

(x²+y²)²⁵-(x²-y²)²⁵

(a+b)ⁿ-(a-b)ⁿ if n is odd

On simplification we get (n+1)/2 terms

i.e. (25+1)/2 = 26/2

= 13

Question 34: The third term of a G.P. is 9. The product of its first five terms i

a. 3⁵

b. 3⁹
c. 3¹⁰
d. 3¹²

Answer:(c)

The third term of G.P. is 9

a.² = 9

Now, the product of five terms = T₁T₂T₃T₄T₅

= (a)(ar)(ar²)(ar³)(ar⁴)

= a⁵r¹⁰

= (ar²)⁵

= (9)⁵

= 3¹⁰

Question 35: A line cuts off equal intercepts on the co-ordinate axes. The angle made by this line with the positive direction of X-axis is

a. 45⁰

b. 90⁰
c. 120⁰
d. 135⁰

Answer:(d)

We know that equation of a line in intercept form is

(x/a)+(y/b) = 1

Here, both intercept are equal

So (x/a)+(y/a) = 1

y = –x+a

Now comparing it with

y = mx + c

We get m = -1 = slope

We know that

Slope = tan θ

tan θ = -1

θ = 135⁰

Question 36:.

∫x3sin⁡3xdx=

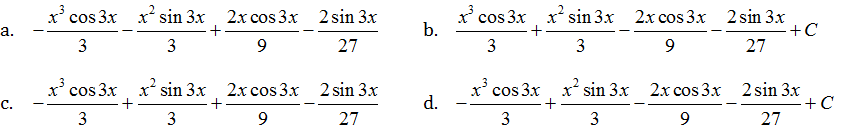
Answer:(c)

Let I =

∫x3sin⁡3xdx

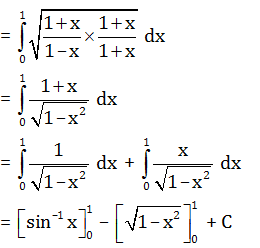
Question 37: The area of the region above X-axis included between the parabola y²= x and the circle x²+y² = 2x in square units is

a. (π/4)-(3/2)

b. (3/2)-( π/4)
c. (2/3)-( π/4)
d. (π/4)-(2/3)

Answer:(d)

y² = x …(1)

x²+ y² = 2x…(2)

(x-1)² +(y-0)² = 1

Equation (2) is a circle with centre (1, 0) and radius 1.

Solving eq.(1) and eq.(2)

(x-1)² + x = 1

x²-x = 0

x(x-1) = 0

x = 0, 1

We get the points of intersection (0, 0) and (1, 1)

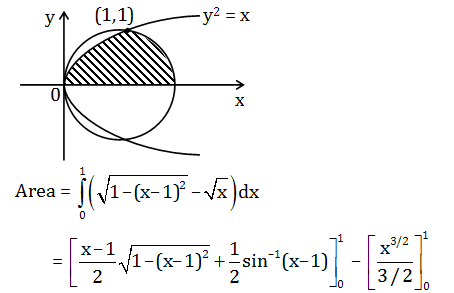
= [0+ π/4]-(2/3)

= (-2/3)+( π/4)

Question 38: The area of the region bounded by Y-axis, y = cos x and y = sin x; 0 ≤x≤π/2 is

a. √2-1 Sq. units

b. √2 Sq. units
c. √2+1 sq. units
d. 2-√2 Sq. units

Answer:(a)

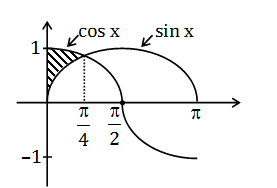
Required area =

∫0π4(cos⁡x−sin⁡x)dx

[cos⁡x−sin⁡x]0π4

= (1/√2)+(1/√2)-1)

= (√2-1) Sq. units

Question 39: The integrating factor of the differential equation (2x+3y²)dy = y dx (y > 0) is

a. e^1/y

b. -1/y²
c. 1/x
d. 1/y²

Answer:(d)

(2x+3y²)dy = y dx

(2x+3y²)/y = dx/dy

(dx/dy)-(2/y)x = 3y

I.F =

e∫−2ydy

= e^{-2 log y}

= y^-2

= 1/y²

Question 40: The equation of the curve passing through the point (1,1) such that the slope of the tangent at any point (x,y) is equal to the product of its coordinates is

a. 2 log x = y²-1

b. 2 log y = x²+1
c. 2 log y = x²-1
d. 2 log x = y²+1

Answer:(c)

(dy/dx) = xy

(1/y)dy = x dx

Integrate

log y = (x²/2)+C ..(i)

Equation (i) passing through (1,2)

log(1) = (1²/2)+C

C = -1/2

Put in (i)

log y = (x²/2)-(1/2)

2 log y = x²-1

Question 41: The eccentricity of the ellipse 9x²+25y² = 225 is

a. 4/5

b. 3/5
c. ¾
d. 9/16

Answer:(a)

9x²+25y² = 225

(x²/5²)+(y²/3²) = 1

Eccentricity (e) = √(a²-b²)/a

= √(25-9)/5

= 4/5

Question 42:

∑r=1n(2r−1)=x

then

limn→∞[13×2+23×2+33×2+…+n3x2]=

a. ½ b. ¼ c. 1 d. 4 Answer:(b)

∑r=1n(2r−1)=x

= (1/4)×1 = 1/4

Question 43: The negation of the statement ”All continuous functions are differentiable.”

a. All continuous functions are not differentiable

b. Some continuous functions are differentiable.
c. Some continuous functions are not differentiable.
d. All differentiable functions are continuous.

Answer:(c)

Always all differentiable functions are continuous. But all continuous functions are not differentiable. So, negation of the given statement is some continuous functions are not differentiable. Ex: |x|

Question 44: Mean and standard deviation of 100 items are 50 and 4 respectively. The sum of all squares of the items is

a. 251600

b. 256100
c. 266000
d. 261600

Answer:(a)

Here n = 100

A = 50

σ = 4

Now A = Σx/n

Σx = An

Σx = 100×50

= 5000

Again from the formula,

σ²+A² = Σx²/n

Σx² = n(σ²+A²)

= 100(16+2500)

= 251600

Question 45: Two letters are chosen from the letters of the word ‘EQUATIONS’. The probability that one is vowel and the other is consonant is

a. 8/9

b. 4/9
c. 3/9
d. 5/9

Answer:(d)

Vowel: E, A, U, I, O ⇒ P(v) = ⁵C₁

Consonant: Q, T, N, S ⇒ P(c) = ⁴C₁

Probability = ⁵C₁× ⁴C₁/⁹C₂

= 5×4/36

= 20/36

= 5/9

Question 46: The constant term in the expansion of

|3x+12x−1x+25x−13x+2x+17x−23x+14x−1|

is:

a. 0

b. 2
c. -10
d. 6

Answer:(d)

Δ=|3x+12x−1x+25x−13x+2x+17x−23x+14x−1|

Put x = 0

Δ=|1−12−121−21−1|

= 1(-3)+1(3)+2(-1+4)

= -3+3+6

= 6

Question 47: If [x] represents the greatest integer function and f(x) = x-[x]-cos x then f’(π/2) =

a. 0

b. 1
c. 2
d. does not exist

Answer:(c)

f(x) = x-[x]-cos x

since x = [x]+{x}

f(x) = {x}-cos x

f’(x) = 1+sin x

f’(π/2) = 1+ sin (π/2)

= 1+1

= 2

Question 48: If

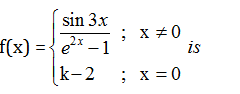
continuous at x=0, then k=

a. 3/2
b. 9/5
c. 1/2
d. 2/3

Answer:(G)

Bonus

*G indicates one grace mark

Question 49: If f(x) = sin^-1[(2^x+1)/(1+4^x)], then f’(0) =

a. 2 log 2
b. log 2
c. (2 log 2)/5
d. (4 log 2)/5
Answer:(b)

f(x) = sin^-1[(2^x+1)/(1+4^x)]

= sin^-1[(2×2^x)/(1+(2^x)²)]

= 2 tan^-1(2^x)

Differentiating w.r.t.x

f’(x) = (2/(1+4^x))(2^x log 2)

f’(0) = (2/(1+1)) log 2

f’(0) = log 2

Question 50: If x = a sec² θ, y = a tan² θ then d²y/dx² =

a. 2a

b. 1
c. 0
d. 4
Answer:(c)

x = a sec² θ

y = a tan² θ

y = a(sec² θ-1)

y = a(x-1)

dy/dx = a

d²y/dx² = 0

Question 51: The inverse of the matrix

[250011−103]

is:

a.[3−11−156−55−22]

b.[3−55−1−6−21−52]

c.[3−155−16−21−52]

d.[3−155−16−21−5−2]

Answer:(c)

Let A =

[250011−103]

|A|=2(3−0)−5(0+1)+0

= 1

A^-1= adj A/|A|

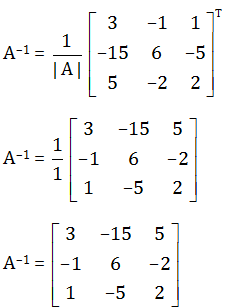
Question 52: If P and Q are symmetric matrices of the same order then PQ-QP is

a. Identity matrix

b. Symmetric matrix
c. zero matrix
d. Skew symmetric matrix

Answer:(d)

Given P = P’ and Q = Q’

Now,

(PQ-QP)’ = (PQ)’-(QP)’

= Q’P’-P’Q’

= QP-PQ

= -[PQ-QP]

So (PQ-QP) is skew-symmetric.

Question 53: If 3A+4B’ =

[7−10170631]

and 2B-3A’ =

[−11840−5−7]

then B = Answer:(a) 3A+4B’ =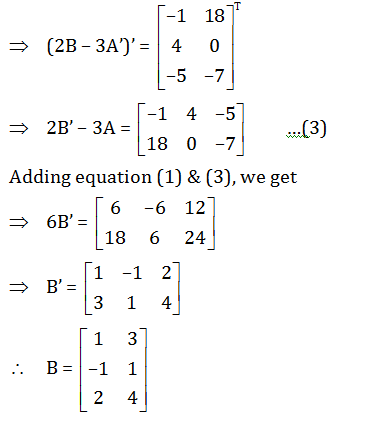

[7−10170631]

..(1) 2B-3A’ =

[−11840−5−7]

..(2)

Question 54: If A =

[1342]

, B =

[2−112]

, then |ABB’|=

a. 50

b. -250
c. 100
d. 250

Answer:(b)

A =

[1342]

B =

[2−112]

B’ =

[21−12]

Now, |ABB’| = |A| |B| |B’|

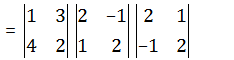
= (2-12)(4+1)(4+1)

= -10×5×5

= -250

Question 55: If the value of a third-order determinant is 16, then the value of the determinant formed by replacing each of its elements by its cofactor is

a. 96

b. 48
c. 256
d. 16

Answer:(c)

Given that |A| = 16

Order of determinant A = 3

Now, |adj A| = |A|²

= 16²

= 256

Question 56:

f:R→R

and

g:[0,∞)→R

is defined by f(x) = x² and g(x) = √x. Which one of the following is not true ?

a. gof (4) = 4

b. fog (-4) = 4
c. fog (2) = 2
d. gof (-2) = 2
Answer:(b)

f(x) = x²

g(x) = √x

Now,

fog(x) = f[g(x)]

= f[√x ]

= x

fog(2) = 2

fog(-4) = -4

And

gof(x) = g[f(x)]

gof(x) = g[x²]

gof(-2) = g(4)

= √4

= 2

Question 57: A = {x|x∈N, x ≤5}, B = {x|x∈Z, x²-5x+6 = 0}, then the number of onto functions from A to B is

a. 2

b. 23
c. 30
d. 32
Answer:(c)

A = {x|x∈N, x ≤5}

A = {1,2,3,4,5}

B = {x|x∈Z, x²-5x+6 = 0}

B = {2,3}

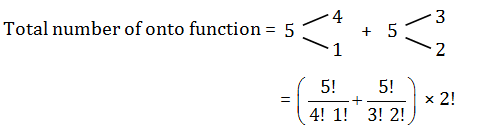
= (5+10)×2

= 30

Question 58: On the set of positive rationals, a binary operation * is defined by a*b = 2ab/5 . If 2*x = 3^-1, then x =

a. 1/6
b. 5/12
c. 2/5
d. 125/48
Answer:(b)

Given condition

a*b = 2ab/5

Now,

2*x = 3^-1

2(2x)/5= 1/3

4x = 5/3

x = 5/12

Question 59: cos[2 sin^-1(3/4)+cos^-1(3/4)] =

a. -3/4
b. 3/4
c. 3/5
d. does not exist
Answer:(a)

cos[2 sin^-1(3/4)+cos^-1(3/4)] = cos [2 sin^-1(3/4)+cos^-1(3/4)]

= cos [sin^-1(3/4)+ sin^-1(3/4)+cos^-1(3/4)]

= cos [(π/2)+sin^-1(3/4)]

= -sin(sin^-1(3/4)

= -3/4

Question 60: If a+ π/2 <2 tan^-1x+3 cot^-1x<b then ‘a’ and ‘b’ are respectively:

a. 0 and π
b. π/2 and 2π
c. 0 and 2π
d. -π/2 and π/2

Answer:(b)

We know that 0 < cot^-1x < π

⇒ π+0<2 (π/2)+ cot^-1x < π+ π

⇒ π<2(tan^-1x+cot^-1x)+cot^-1x<2π

⇒ π<2tan^-1x+3cot^-1x<2π ..(1)

compare equation (1) to a+ π/2 <2 tan^-1x+3 cot^-1x<b

a = π/2

b = 2π

Talk to our expert

+91 74112 69409

Request call back

KCET 2019 Maths Paper with Solutions

Introduction to KCET 2019 Maths Paper

Detailed Analysis of KCET 2019 Maths Paper

Algebra

Trigonometry

Calculus

Geometry

Talk to our expert

Contact

Company

Useful links

Support

KCET 2019 Maths Paper with Solutions

Introduction to KCET 2019 Maths Paper

Detailed Analysis of KCET 2019 Maths Paper

Algebra

Trigonometry

Calculus

Geometry

Talk to our expert

Contact

Company

Useful links

Support

Login with your site account

Login with your site account